Question

Write y = x2 + 24x + 144 as a square of binomial.

Answer 1

`y=(x+12)^2\\`

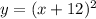
Explanation:

To write a quadratic equation into binomial form we can compare the equation into the completing square form of a quadratic equation like this ,

`y=a(x-h)^2+k`

now since,

`y=x^2+24x+144`

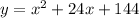
we can equate both the equations from left hand side to right hand side like this,

`x^2+24x+144=a(x-h)^2+k\\`

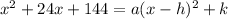
now we solve,

`x^2+24x+144=a(x-h)^2+k\\x^2+24x+144=a((x)^2-2(x)(h)+(h)^2)+k\\x^2+24x+144=a(x^2-2hx+h^2)+k\\x^2+24x+144=ax^2-2ahx+ah^2+k\\`

now we compare the coefficients of x^2:

`1 = a\\`

now we compare the coefficients of x :

`24=-2ah\\24=-2(1)h\\24=-2h\\(24)/(-2)=h\\-12=h\\`

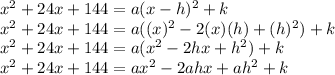
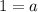
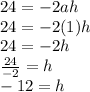
now we compare the constants , (constants are the letters which are not associated with any variable in this case the variable is x)

`144 = ah^2+k\\144=(1)(-12)^2+k\\144=(1)(144)+k\\144=144+k\\144-144=k\\0=k\\`

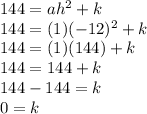
so now the value we got all the values for the completing square form we plug those in , a = 1 , h = -12 , k = 0 ,

`y=a(x-h)^2+k\\y=1(x-(-12))^2+0\\y=(x+12)^2\\`

this is the square of a binomial, if you want to verify if we expands this formula by the formula of (a + b)^2 we would get the same result. Thus this is the correct answer.