Question

Two gears are adjusted so that the smaller gear drives the larger one. if the smaller gear of 3.7cm rotates through an angle of 300° through how many degrees does the larger gear of 7.1cm rotate

please help me

Answer 1

The larger gear will rotate through 156°

Explanation:

Arc Length

The arc length S of an angle θ on a circle of radius r is:

`S = \theta r`

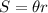
Where θ is expressed in radians.

The smaller gear of r1=3.7 cm drives a larger gear of r2=7.1 cm. The smaller gear rotates through an angle of θ1=300°.

Convert the angle to radians:

`\displaystyle \theta_1=300*(\pi)/(180)=(5\pi)/(3)`

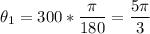
The arc length of the smaller gear is:

`\displaystyle S_1=(5\pi)/(3)\cdot 3.7`

`\displaystyle S_1=(18.5\pi)/(3)`

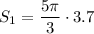
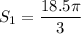
The larger gear rotates the same arc length, so:

`\displaystyle S_2=(18.5\pi)/(3)`

`\displaystyle \theta_2\cdot r_2=(18.5\pi)/(3)`

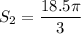
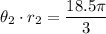
Solving for θ2:

`\displaystyle \theta_2=(18.5\pi)/(3r_2)`

`\displaystyle \theta_2=(18.5\pi)/(3*7.1)`

`\theta_2=2.73\ radians`

`\displaystyle \theta_2=2.73*(180)/(\pi)=156`

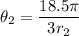
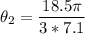
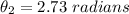
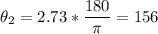
The larger gear will rotate through 156°