Answer:
The larger gear will rotate through 156°
Explanation:
Arc Length
The arc length S of an angle θ on a circle of radius r is:
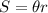
Where θ is expressed in radians.
The smaller gear of r1=3.7 cm drives a larger gear of r2=7.1 cm. The smaller gear rotates through an angle of θ1=300°.
Convert the angle to radians:

The arc length of the smaller gear is:
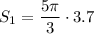
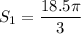
The larger gear rotates the same arc length, so:
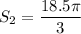
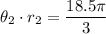
Solving for θ2:
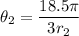
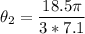
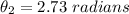
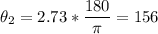
The larger gear will rotate through 156°