Question

Which of the following statements have the same result? Explain each step in solving each one.

I. f(2) when f(x) = 3x + 4
II. f−1(4) when f(x) =3x-4/5
III. 3y − 6 = y + 10
You must solve each and show and explain each step. Then explain equivalency. Part 2 you must find the inverse equation.

Answer 1

None of the following statements have the same result.

Explanation:

1) f(2) when f(x) = 3x + 4

We just have to put x=2

`f(x)=3x+4\\f(2)=3(2)+4\\f(2)=6+4\\f(2)=10`

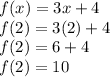
So, f(2) when f(x) = 3x + 4 is x=10

2) f⁻¹ (4) when f(x) =3x-4/5

We need to find f⁻¹(x) first.

Put
`y=3x-(4)/(5)`

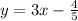
Now solve for x

Add 4/5 on both sides

`y+(4)/(5)=3x-(4)/(5)\\y+(4)/(5)=3x\\x=(1)/(3)y+(4)/(5*3)\\x=(1)/(3)y+(4)/(15)\\x=(5y+4)/(15)`

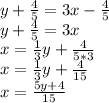
Now put f⁻¹(x) instead of x and replace y with x

`f^(-1)(x)=(5x+4)/(15)`

Now finding f⁻¹(4)

`f^(-1)(x)=(5x+4)/(15) \\f^(-1)(4)=(5(4)+4)/(15) \\f^(-1)(4)=(20+4)/(15) \\f^(-1)(4)=(24)/(15)`

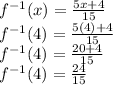
f⁻¹ (4) when f(x) =3x-4/5 is 24/15

3)
`3y - 6 = y + 10\\`

Solving:

`3y - 6 = y + 10\\3y-y=10+6\\2y=16\\y=16/2\\y=8`

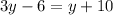
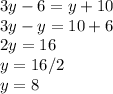
Solving 3y − 6 = y + 10, we get y=8

None of the following statements have the same result.