Answer:
x = 0 or x = 1
Step-by-step explanation:
Given equation:
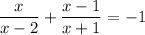
Multiply the two denominators to get the same denominator:
Multiply the numerator of the first fraction by the denominator of the second fraction to get the new numerator of the first fraction.
Multiply the numerator of the second fraction by the denominator of the first fraction to get the new numerator of the second fraction.
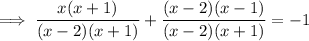
Add the numerators and keep the denominator so that there is now one fraction:
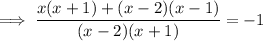
Simplify the numerator by expanding the brackets:
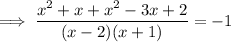
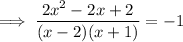
Simplify the denominator by expanding the brackets:
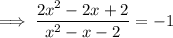
Multiply both sides by the denominator of the left side:
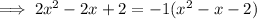
Simplify and move everything to the left side:
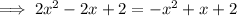
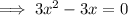
Factor:
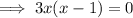
Therefore:
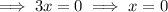
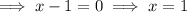
Therefore, x = 0 or x = 1