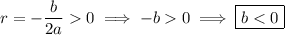The differential equation
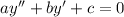
has characteristic equation
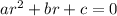
with roots
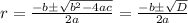 .
.
• If
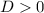 , the roots are real and distinct, and the general solution is
, the roots are real and distinct, and the general solution is
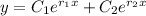
• If
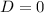 , there is a repeated root and the general solution is
, there is a repeated root and the general solution is
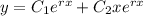
• If
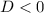 , the roots are a complex conjugate pair
, the roots are a complex conjugate pair
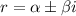 , and the general solution is
, and the general solution is
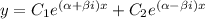
which, by Euler's identity, can be expressed as
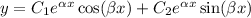
The solution curve in plot (A) has a somewhat periodic nature to it, so
 . The plot suggests that
. The plot suggests that
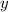 will oscillate between -∞ and ∞ as
will oscillate between -∞ and ∞ as
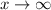 , which tells us
, which tells us
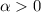 (otherwise, if
(otherwise, if
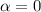 the curve would be a simple bounded sine wave, or if
the curve would be a simple bounded sine wave, or if
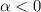 the curve would still oscillate but converge to 0). Since
the curve would still oscillate but converge to 0). Since
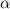 is the real part of the characteristic root, and we assume
is the real part of the characteristic root, and we assume
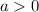 , we have
, we have
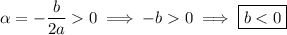
Since
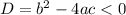 , we have
, we have
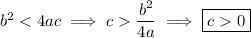
The solution curve in plot (B) is not periodic, so
 . For
. For
 near 0, the exponential terms behave like constants (i.e.
near 0, the exponential terms behave like constants (i.e.
 ). This means that
). This means that
• if
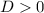 , for some small neighborhood around
, for some small neighborhood around
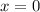 , the curve is approximately constant,
, the curve is approximately constant,
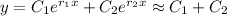
• if
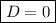 , for some small neighborhood around
, for some small neighborhood around
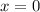 , the curve is approximately linear,
, the curve is approximately linear,
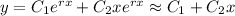
Since
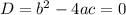 , it follows that
, it follows that
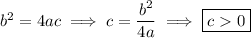
As
 , we see
, we see
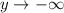 which means the characteristic root is positive (otherwise we would have
which means the characteristic root is positive (otherwise we would have
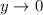 ), and in turn
), and in turn