Question

If point A (4, -3) is translated 3 units horizontally and -5 units vertically, rotated 90° clockwise, reflected over the x-axis, and dilated by a factor of 5: a) What is the rule (written using proper symbols)? b) What are the coordinates of A'?

Answer 1

Given:

Point A (4, -3) is translated 3 units horizontally and -5 units vertically, rotated 90° clockwise, reflected over the x-axis, and dilated by a factor of 5.

To find:

The rule and coordinates of A'.

Solution:

Let a point be P(x,y).

If a point translated 3 units horizontally and -5 units vertically, then

`P(x,y)\to P_1(x+3,y-5)`

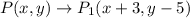
Then, rotated 90° clockwise.

`(x,y)\to (y,-x)`

`P_1(x+3,y-5)\to P_2(y-5,-(x+3))`

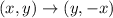
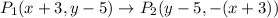
Then, reflected over the x-axis.

`(x,y)\to (x,-y)`

`P_2(y-5,-(x+3))\to P_3(y-5,x+3)`

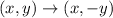
Dilated by a factor of 5.

`(x,y)\to (5x,5y)`

`P_3(y-5,x+3)\to P'(5(y-5),5(x+3))`

`P_3(y-5,x+3)\to P'(5y-25,5x+15)`

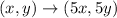
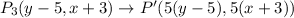
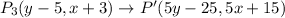
So, the rule of transformation is

`(x,y)\to (5y-25,5x+15)`

We have a point A(4,-3). So, put x=4 and y=-3.

`A(x,y)\to A'(5(-3)-25,5(4)+15)`

`A(x,y)\to A'(-15-25,20+15)`

`A(x,y)\to A'(-40,35)`

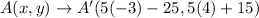
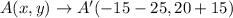
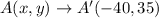
Therefore, the coordinate of point A' are (-40,35).