Answer: Choice A)
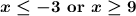
===================================================
Step-by-step explanation:
Let's solve the first inequality mentioned.
To do so, divide both sides by 6.
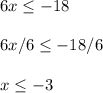
The inequality sign stays the same the entire time. It only flips if we divided both sides by a negative number.
Through similar steps, this is how we'd solve the second inequality given:
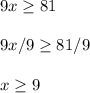
So overall
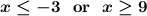
The key word "or" is important. If it was "and", then we'd have no solutions because no such number is both smaller than -3 and also larger than 9 at the same time.
The graph of this on the number line will involve closed circles at -3 and 9. Then we shade anything that is not between those closed circles.