Answer:
The second distance of the sound from the source is 431.78 m..
Step-by-step explanation:
Given;
first distance of the sound from the source, r₁ = 1.48 m
first sound intensity level, I₁ = 120 dB
second sound intensity level, I₂ = 70.7 dB
second distance of the sound from the source, r₂ = ?
The intensity of sound in W/m² is given as;
![dB = 10 Log[(I)/(I_o) ]\\\\For \ 120 dB\\\\120 = 10Log[(I)/(1*10^(-12))]\\\\12 = Log[(I)/(1*10^(-12))]\\\\10^(12) = (I)/(1*10^(-12))\\\\I = 10^(12) \ * \ 10^(-12)\\\\I = 1 \ W/m^2](https://img.qammunity.org/2021/formulas/physics/college/mm6x1p2zxizljqwoql16hxfbtu5mvn86yq.png)
![For \ 70.7 dB\\\\70.7 = 10Log[(I)/(1*10^(-12))]\\\\7.07 = Log[(I)/(1*10^(-12))]\\\\10^(7.07) = (I)/(1*10^(-12))\\\\I = 10^(7.07) \ * \ 10^(-12)\\\\I = 1 * \ 10^(-4.93) \ W/m^2](https://img.qammunity.org/2021/formulas/physics/college/ygi8icf0o78ajmnp7seem8awue0f8mn2cz.png)
The second distance, r₂, can be determined from sound intensity formula given as;
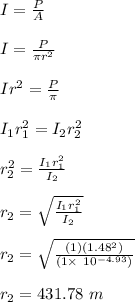
Therefore, the second distance of the sound from the source is 431.78 m.