Question

The sound level at a distance of 1.48 m from a source is 120 dB. At what distance will the sound level be 70.7 dB?

Answer 1

The second distance of the sound from the source is 431.78 m..

Step-by-step explanation:

Given;

first distance of the sound from the source, r₁ = 1.48 m

first sound intensity level, I₁ = 120 dB

second sound intensity level, I₂ = 70.7 dB

second distance of the sound from the source, r₂ = ?

The intensity of sound in W/m² is given as;

`dB = 10 Log[(I)/(I_o) ]\\\\For \ 120 dB\\\\120 = 10Log[(I)/(1*10^(-12))]\\\\12 = Log[(I)/(1*10^(-12))]\\\\10^(12) = (I)/(1*10^(-12))\\\\I = 10^(12) \ * \ 10^(-12)\\\\I = 1 \ W/m^2`

`For \ 70.7 dB\\\\70.7 = 10Log[(I)/(1*10^(-12))]\\\\7.07 = Log[(I)/(1*10^(-12))]\\\\10^(7.07) = (I)/(1*10^(-12))\\\\I = 10^(7.07) \ * \ 10^(-12)\\\\I = 1 * \ 10^(-4.93) \ W/m^2`

The second distance, r₂, can be determined from sound intensity formula given as;

`I = (P)/(A)\\\\I = (P)/(\pi r^2)\\\\Ir^2 = (P)/(\pi )\\\\I_1r_1^2 = I_2r_2^2\\\\r_2^2 = (I_1r_1^2)/(I_2) \\\\r_2 = \sqrt{(I_1r_1^2)/(I_2)} \\\\r_2 = \sqrt{((1)(1.48^2))/((1 * \ 10^(-4.93)))}\\\\r_2 = 431.78 \ m`

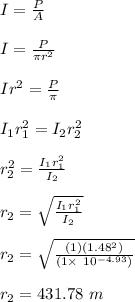
Therefore, the second distance of the sound from the source is 431.78 m.