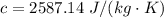Question

An unknown material, m1 = 0.41 kg, at a temperature of T1 = 86 degrees C is added to a Dewer (an insulated container) which contains m2 = 1.7 kg of water at T2 = 22 degrees C. Water has a specific heat of cw = 4186 J/(kg⋅K). After the system comes to equilibrium the final temperature is T = 30.3 degrees C.

Answer 1

Complete Question

An unknown material, m1 = 0.41 kg, at a temperature of T1 = 86 degrees C is added to a Dewer (an insulated container) which contains m2 = 1.7 kg of water at T2 = 22 degrees C. Water has a specific heat of cw = 4186 J/(kg⋅K). After the system comes to equilibrium the final temperature is T = 30.3 degrees C.

Part (a) Input an expression for the specific heat of the unknown material.

Part (b) What is the specific heat in J/(kg⋅K)?

Answer:

a

`c = (m_2 * c_w (T - T_2))/(m_1 * (T_1 - T) )`

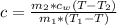
b

`c = 2587.14 \ J /(kg \cdot K)`

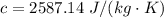
Step-by-step explanation:

From the question we are told that

The mass of the material is
`m_1 = 0.41 \ kg`

The temperature is
`T_1 = 86 ^oC`

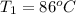
The mass of water is
`m_2 = 1.7 \ kg`

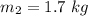
The temperature of water is
`T_2 = 22^oC`

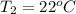
The specific heat of water is
`c_w = 4186 \ J/(kg\cdot K)`

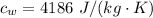
The temperature of the system is
`T= 30 .3^o C`

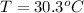
Generally heat lost by the unknown material = heat gained by water

Generally the heat gained by water is mathematically represented as

`Q_2= m_2 * c_w (T - T_2)`

=>
`Q_2= 1.7 * 4186 (30.3 - 22)`

=>
`Q_2= 59064.46 \ J`

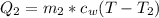
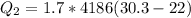
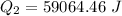
Generally the heat lost by the unknown material is mathematically represented as

`Q_1= m_1 * c* (T_1 - T)`

`m_2 * c_w (T - T_2) = m_1 * c* (T_1 - T)`

=>
`c = (m_2 * c_w (T - T_2))/(m_1 * (T_1 - T) )`

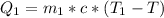
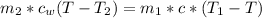
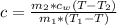
Here c is the specific heat capacity of the unknown material

=>
`Q_1= 0.41 * c (86 - 30.3)`

=>
`Q_1= 22.83 c`

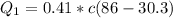
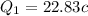
So

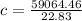
`59064.46 = 22.83 c`

=>
`c = (59064.46 )/( 22.83)`

=>
`c = 2587.14 \ J /(kg \cdot K)`