Given:
A linear function starting at point C at (3, –2) and ending at point D at (–2, 3).
To find:
The rate of change and the initial value.
Solution:
If a linear function passes through two points
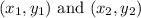 , then the equation of linear function is
, then the equation of linear function is
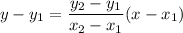
The given linear function passes through (3,-2) and (-2,3). So, the equation is

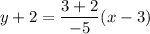

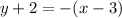
Subtracting 2 on both sides, we get
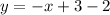

On comparing this equation with slope intercept form
 , where, m is slope and b is y-intercept, we get
, where, m is slope and b is y-intercept, we get
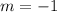 and
and
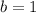
Therefore, the rate of change is -1 and the initial value is 1.