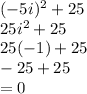Question

shasta claimed that the equation x^2+25=0 can be solved by using its factored form of (x+5i)^2=0, and that -5i is the only zero for this function. which statement is true?

Answer 1

The given equation will have two roots as +5i and -5i

Explanation:

Shasta claimed that the equation x^2+25=0 can be solved by using its factored form of (x+5i)^2=0, and that -5i is the only zero for this function

The given equation is
`x^2+25 =0`

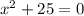
This clearly shows it will have complex roots, and since it is a quadratic equation it will have 2 complex roots

`x^2 = -25 \\x = √(-25) \\x= √(-1)* √(25)\\`

`x = i√(25)`

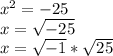
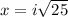
x = ± 5i

It will be false to say that -5i will be the only complex root to this equation.

The given equation will have +5i and -5i as its roots.

Lets verify

x = +5i

`(5i)^2 + 25 \\25i^2 + 25 \\25(-1) + 25\\-25 + 25 = 0`

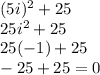
x = -5i

`(-5i)^2 + 25 \\25i^2 + 25 \\25(-1) + 25 \\-25 + 25 \\ = 0`