Answer:
a. k = 24 b. y =

Explanation:
a. Find the value of the constant k
Since
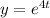 is a solution of d²y/dt² -10dy/dt + ky = 0, then
is a solution of d²y/dt² -10dy/dt + ky = 0, then
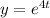 must satisfy the equation.
must satisfy the equation.
So, d²y/dt² =
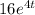 and dy/dt =
and dy/dt =
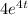
So, d²y/dt² -10dy/dt + ky = 0
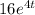 - 10(
- 10(
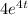 ) + k(
) + k(
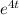 ) = 0
) = 0
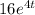 -
-
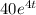 +
+
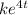 = 0
= 0
-
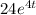 +
+
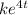 = 0
= 0
-
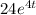 = -
= -
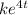
So, k = 24
b. Find the general solution to this equation.
Since k = 24, our equation is
d²y/dt² -10dy/dt + 24y = 0
The characteristic equation is thus
m² - 10m + 24 = 0
Factorizing this we have
m² - 6m - 4m + 24 = 0
m(m - 6) - 4(m - 6) = 0
(m - 6)(m - 4) = 0
m - 6 = 0 or m - 4 = 0
m = 6 or m = 4
Since we have real roots for the characteristic equation, then, the general solution is
y =
