Answer:
a) α = -65,2 rad/s².
b) t = 2,57 s.
Step-by-step explanation:
a) La aceleración angular se puede calcular usando la siguiente ecuación:
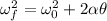
En donde:
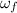 : es la velocidad angular final = 2000 rpm = 209,4 rad/s
: es la velocidad angular final = 2000 rpm = 209,4 rad/s
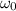 : es la velocidad angular inicial = 3600 rpm = 377,0 rad/s
: es la velocidad angular inicial = 3600 rpm = 377,0 rad/s
α: es la aceleración angular=?
θ: es el desplazamiento o número de vueltas = 120 rev = 754,0 rad
Las conversiones de unidades se hicieron sabiendo que 1 revolución = 2π radianes y que 1 minuto = 60 segundos.
Resolviendo la ecuación (1) para α, tenemos:
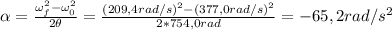
Entonces, la aceleración angular es -65,2 rad/s². El signo negativo se debe a que el motor está desacelerando.
b) El tiempo transcurrido se puede encontrar como sigue:
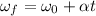
Resolviendo para t, tenemos:
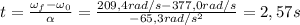
Por lo tanto, el tiempo transcurrido fue 2,57 s.
Espero que te sea de utilidad!