Answer:
The equation that models the situation is
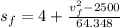 .
.
Explanation:
Let suppose that effects from air friction and Earth's rotation can be neglected, so that the softball can be modelled experiment a free fall, that is, an uniform accelerated motion due to gravity. From we know the initial velocity and position of the position and we can determine the final position of the ball as a function of the final velocity:
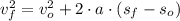 (1)
(1)
Where:
 ,
,
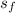 - Initial and final position of the softball, measured in feet.
- Initial and final position of the softball, measured in feet.
 - Acceleration, measured in meters per square second.
- Acceleration, measured in meters per square second.
 ,
,
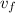 - Initial and final velocities of the softball, measured in feet per second.
- Initial and final velocities of the softball, measured in feet per second.
If we know that
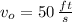 ,
,
 and
and
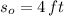 , then the equation that models the situation is:
, then the equation that models the situation is:
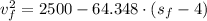
Then, we clear the final position of the softball:
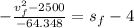
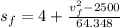
The equation that models the situation is
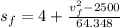 .
.