Question

A golfer shoots a ball horizontally off a cliff with a speed of 80.0 m/s, and it lands 471m from the base of the cliff.

1. How long is the golf ball in the air?
2. What is the height of the cliff?
3. What is the golf ball/s speed when it lands?

Answer 1

1. t = 5.89 s

2. h = 170 m

3. Vf = 57.8 m/s

Step-by-step explanation:

1.

First, we analyze the horizontal motion of the golf ball. Assuming the air friction to be negligible, the horizontal motion will be uniform. So, e can use the following equation:

`s = vt`

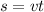
where,

s = horizontal distance covered by the golf ball = 471 m

v = horizontal speed of golf ball = 80 m/s

t = time taken by the golf ball in air = ?

Therefore,

`471\ m = (80\ m/s)t\\\\t = (471\ m)/(80\ m/s)\\\\`

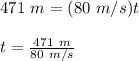
t = 5.89 s

2.

Now, we analyze the vertical motion. Using 2nd equation of motion:

`h = v_(i)t + (1)/(2)gt^2`

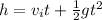
where,

h = height of cliff = ?

vi = vertical component of initial speed of ball = 0 m/s(ball was shot horizontally)

g = acceleration due to gravity = 9.81 m/s²

t = time of flight = 5.89 s

Therefore,

`h = (0\ m/s)(5.89\ s) + (1)/(2)(9.81\ m/s^2)(5.89\ s)^2`

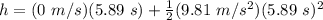
h = 170 m

3.

Now, we can use 1st equation of motion:

`v_(f) = v_(i) + gt\\v_(f) = 0 m/s + (9.81\ m/s^2)(5.89\ s)\\`

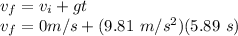
Vf = 57.8 m/s