Line M passes through the points (-5, 8) and (-1, 9) what is true of line M

Question

asked Jan 11, 2021 145k views

1 Answer

Bajju · Answer 1 · 2021-01-15T13:56:10+0000

Answer:

The equation of the line is:

Explanation:

Given the points

Finding the slope between the points

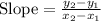
$\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

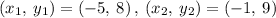
$\left(x_1,\:y_1\right)=\left(-5,\:8\right),\:\left(x_2,\:y_2\right)=\left(-1,\:9\right)$

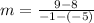
$m=(9-8)/(-1-\left(-5\right))$

m=(1)/(4)

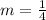
Using the point-slope form of the line equation

$y-y_1=m\left(x-x_1\right)$

substituting the values m = 1/4 and the point (-5, 8)

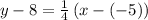
$y-8=(1)/(4)\left(x-\left(-5\right)\right)$

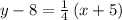
$y-8=(1)/(4)\left(x+5\right)$

Add 8 to both sides

$y-8+8=(1)/(4)\left(x+5\right)+8$

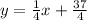
y=(1)/(4)x+(37)/(4)

Thus, the equation of the line is: