Question

What is the 10th term of the sequence 729, 243, 81, 27...? Enter any rational answer

in the form a/b or round to the nearest thousandth.

Help please.

Answer 1

The 10th term of the sequence is:

• 
  `a_(10)=(1)/(27)`

Explanation:

Given the number

729, 243, 81, 27...

A geometric sequence has a constant ratio 'r' and is defined by

`a_n=a_0\cdot r^(n-1)`

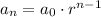
Computing the ratio of all the adjacent terms

`(243)/(729)=(1)/(3),\:\quad (81)/(243)=(1)/(3),\:\quad (27)/(81)=(1)/(3)`

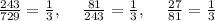
The ratio of all the adjacent terms is the same and equal to

`r=(1)/(3)`

also

`a_1=729`

Therefore, the nth term is computed by:

`a_n=729\left((1)/(3)\right)^(n-1)`

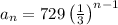
Putting n = 10 to find the 10th term

`a_(10)=729\left((1)/(3)\right)^(10-1)`

`=729\cdot (1)/(3^9)`

`=(1\cdot \:729)/(3^9)`

`=(729)/(3^9)`

`=(3^6)/(3^9)`

`=(1)/(3^3)`

`a_(10)=(1)/(27)`

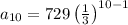
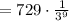
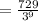
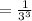
Therefore, the 10th term of the sequence is:

• 
  `a_(10)=(1)/(27)`