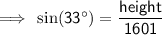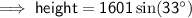Answer:
A. 871.97 m
Explanation:
Model this is a right triangle.
Use the sine trigonometric ratio to find the height of the weather balloon from the ground.
Sine trigonometric ratio
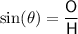
where:
 is the angle
is the angle- O is the side opposite the angle
- H is the hypotenuse (the side opposite the right angle)
Given:
 = 33°
= 33°- O = height
- H = 1601 m
Substitute the given values into the formula and solve for O: