Answer:
Explanation:
rewrite 9-6x+
 as
as
 -6x+9. (this step isn't necessary, but it's easier when the bigger term is in front)
-6x+9. (this step isn't necessary, but it's easier when the bigger term is in front)
There's two ways: using the quadratic formula, or just doing it in your head (for simple ones)
For the simple way:
think about what numbers not only multiply to equal c (represented by 9 in this case) but also add to equal -6 (represents b in this problem). There are two numbers for this problem that work: -3 and -3. So you would write the factored form as (x-3)(x-3)
Quadratic formula:
The formula is
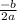 ±
±
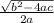
This formula works for equations in the form of a
 +bx+c.
+bx+c.
Substitute in the values to get:
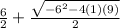
simplify:
3±

3±
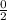
the answer is 3, which is the x-intercept. Write that as (x-3)(x-3)