Question

Write the equation, in slope-intercept form, of the line that passes through (-2,0) and is parallel to the line represented by 5x-3y=-17 .

Answer 1

`y=(5)/(3)x+(10)/(3)`

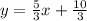
Explanation:

Firstly we rewrite the equation that is parallel to the line we need because parallel lines have the same slope by the rule

`m_1=m_2`

so we rewrite the equation in slope-intercept form:

`5x-3y=17\\-3y=-5x+17\\y=(-5x+17)/(-3)\\\\y=(-5x)/(-3)+(17)/(-3) \\\\y=(5)/(3)x-(17)/(3)`

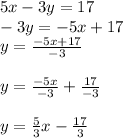
and now we compare it with our slope-intercept form equation:

`y=mx+b`

the coefficient of x which is m is the slope and since parallel lines have equal slopes the line that we need would also have the same slope which is 5/3.

now the next step is the line that we need passes through the point (-2,0) so it means that it should satisfy that specific point so we insert that point into our slope-intercept form and insert the slope which is 5/3 which is m.

`y=mx+b\\y=(5)/(3)x+b\\\\0=(5)/(3)(-2)+b\\\\0=(-10)/(3)+b\\\\b=(10)/(3)\\`

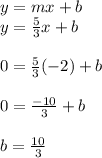
now we know that the y-intercept(b) of the line we need is 10/3 and slope(m) is 5/3 insert these values into our slope-intercept form:

`y=mx+b\\y=(5)/(3)x+(10)/(3) \\`

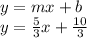
so this is our given line.