Answer:
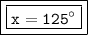
Explanation:
To solve this problem we need to apply the triangle exterior angle property.
*Exterior angle of a triangle is equal to the sum of its two opposite interior angles.*
146 ° here, is an exterior angle of the triangle, and 21 °/x are opposite interior angles.
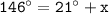
Switch sides:
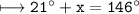
Subtract 21 from both sides:
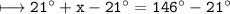
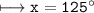
________________________________