Answer:
4 seconds
Explanation:
Given
Ann has an empty cup and add 1 ounce of water per second
let the number of seconds required to fill the cup be x
let the total be y
in x seconds Ann will have x ounces of water in the cup.
so the total amount of water in Ann's cup will be

Bob has 12 ounces of water and drinks 2 ounces per second
also, let the number of seconds required to empty the cup be x
let the total be y
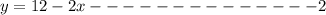
Step two:
equate the two equations above and solve for x
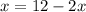
collect like terms
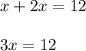
divide both sides by 3
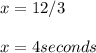
Therefore, after about 4 seconds Ann and Bob's cup will have the same amount of water