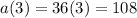Question

asked Oct 7, 2023 136k views

1 Answer

Tomy · Answer 1 · 2023-10-11T08:41:30+0000

Explanation:

Know that

The derivative of position with respect of t is velocity.

Or if you want to say

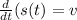
(d)/(dt) (s(t) = v

Or in the form of the definition of the derivative

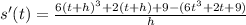
$s'(t) = \frac{6 (t + h) {}^(3) + 2(t + h) + 9 - (6 {t}^(3) + 2t + 9) }{h}$

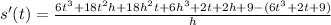
$s'(t) = \frac{6 {t}^(3) + 18t {}^(2)h + 18h {}^(2) t + 6 {h}^(3) + 2t + 2h + 9 - (6 {t}^(3) + 2t + 9)}{h}$

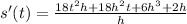
$s'(t) = \frac{18 {t}^(2)h + 18h {}^(2)t + 6h {}^(3) + 2h }{h}$

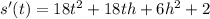
$s'(t) = 18 {t}^(2) + 18th + 6h {}^(2) + 2$

Let h be a small number, so we can cancel out small things.

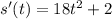
$s'(t) = 18 {t}^(2) + 2$

We know the derivative of position is velocity

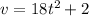
$v = 18 {t}^(2) + 2$

So the velocity at time t is

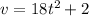
$v = 18 {t}^(2) + 2$

Plug in 3 for t to find the velocity

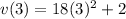
$v(3) =18(3) {}^(2) + 2$

v(3) = 164

So the velocity at t=3, is 164.

Next, the derivative of velocity is acceleration so

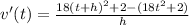
$v'(t) = \frac{18(t + h) {}^(2) + 2 - (18 {t}^(2) + 2)}{h}$

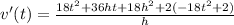
$v'(t) = \frac{18 {t}^(2) + 36ht + 18 {h}^(2) + 2(- 18 {t}^(2) + 2 ) }{h}$

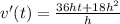
$v'(t) = \frac{36ht + 18 {h}^(2) }{h}$

Divide by h.

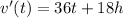
v'(t) = 36t + 18h

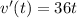
v'(t) = 36t

The derivative of velocity is acceleration so

a = 36t

The acceleration in time t is

36t

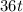
To find acceleration, plug in 3 for t.

a(3) = 36( 3) = 108

Please log in or register to add a comment.