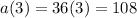Explanation:
Know that
The derivative of position with respect of t is velocity.
Or if you want to say
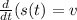
Or in the form of the definition of the derivative
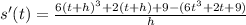
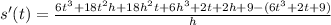
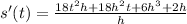
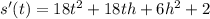
Let h be a small number, so we can cancel out small things.
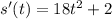
We know the derivative of position is velocity
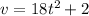
So the velocity at time t is
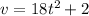
Plug in 3 for t to find the velocity
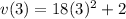
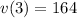
So the velocity at t=3, is 164.
Next, the derivative of velocity is acceleration so
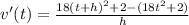
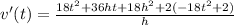
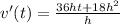
Divide by h.
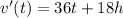
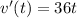
The derivative of velocity is acceleration so
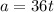
The acceleration in time t is
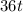
To find acceleration, plug in 3 for t.