Answer:
The new intensity becomes (1/9) of the initial intensity.
Step-by-step explanation:
A source radiates sound uniformly in all directions and its intensity is proportional to the distance as follows :
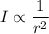
Let I₁ and I₂ be the intensities at a distance r₁ and r₂. So,
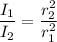
We have, r₂ = 3r₁
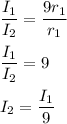
Hence, the new intensity becomes (1/9) of the initial intensity.