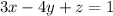Question

Find an equation of the plane with the given characteristics. The plane passes through the points (4, 3, 1) and (4, 1, -7) and is perpendicular to the plane 8x 7y 4z

Answer 1

`3x - 4y + z = 1`

Explanation:

Given

`Point\ 1 = (4,3,1)`

`Point\ 2 = (4,1,-7)`

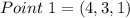
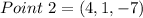
Perpendicular to
`8x + 7y + 4z = 18`

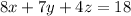
Required

Determine the plane equation

The general equation of a plane is:

`a(x-x_1) + b(y - y_1) + c(z-z_1) = 0`

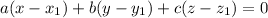
For
`n = <a,b,c>`

`(x_1,y_1,z_1) = (4,3,1)`

`(x_2,y_2,z_2) = (4,1,-7)`

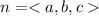
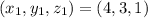
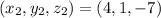
First, we need to determine parallel vector
`V_1`

`V_1 = <x_1 - x_2, y_1 - y_2, z_1 - z_2>`

`V_1 = <4 - 4, 3 - 1, 1 - (-7)>`

`V_1 = <0,2,8>`

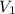
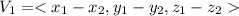
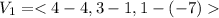
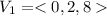
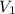`V_1` is parallel to the required plane

From the question, the required plane is perpendicular to
`8x + 7y + 4z = 18`

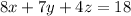
Next, we determine vector
`V_2`

`V_2 = <8,7,4>`

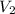
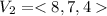
This implies that the required plane is parallel to
`V_2`

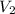
Hence:
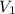`V_1` and
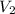`V_2` are parallel.

So, we can calculate the cross product
`V_1 * V_2`

`V_1 = <0,2,8>`

`V_2 = <8,7,4>`

`n = V_1 * V_2`

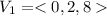
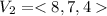
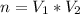
`V_1 * V_2 =\left[\begin{array}{ccc}i&j&k\\0&2&8\\8&7&4\end{array}\right]`

The product is always of the form + - +

So:

`V_1 * V_2 = i\left[\begin{array}{cc}2&8\\7&4\end{array}\right]`
`-j\left[\begin{array}{cc}0&8\\8&4\end{array}\right]`
`+k\left[\begin{array}{cc}0&2\\8&7\end{array}\right]`

Calculate the product

`V_1 * V_2 = i(2*4- 8*7) - j(0*4- 8*8) + k(0*7 - 2 * 8)`

`V_1 * V_2 = i(8- 56) - j(0- 64) + k(0 - 16)`

`V_1 * V_2 = i(-48) - j(- 64) + k(- 16)`

`V_1 * V_2 = -48i +64j - 16k`

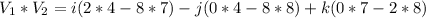
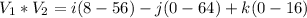
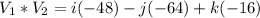
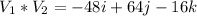
So, the resulting vector, n is:

`n = <-48,64,-16>`

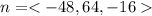
Recall that:

`n = <a,b,c>`

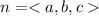
By comparison:

`a = -48`
`b = 64`
`c = -16`

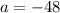
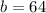
Substitute these values in
`a(x-x_1) + b(y - y_1) + c(z-z_1) = 0`

`-48(x-x_1) + 64(y - y_1) -16(z-z_1) =0`

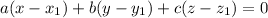
Recall that:
`(x_1,y_1,z_1) = (4,3,1)`

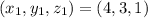
So, we have:

`-48(x-4) + 64(y - 3) -16(z-1) =0`

`-48x + 192 + 64y -192 - 16z +16 = 0`

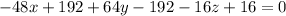
Collect Like Terms

`-48x + 64y - 16z = 0 - 192 + 192 - 16`

`-48x + 64y - 16z = -16`

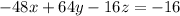
Divide through by -16

`3x - 4y + z = 1`

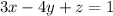
Hence, the equation of the plane is
`3x - 4y + z = 1`