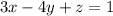Answer:
Explanation:
Given
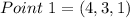
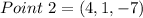
Perpendicular to
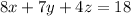
Required
Determine the plane equation
The general equation of a plane is:
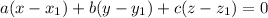
For
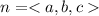
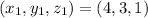
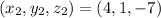
First, we need to determine parallel vector
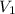
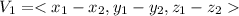
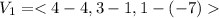
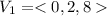
 is parallel to the required plane
is parallel to the required plane
From the question, the required plane is perpendicular to
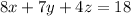
Next, we determine vector
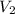
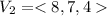
This implies that the required plane is parallel to
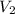
Hence:
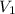 and
and
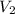 are parallel.
are parallel.
So, we can calculate the cross product

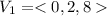
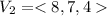
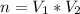
![V_1 * V_2 =\left[\begin{array}{ccc}i&j&k\\0&2&8\\8&7&4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/gbfityc9fi89waqddx47mjqevn0vabxo9y.png)
The product is always of the form + - +
So:
![V_1 * V_2 = i\left[\begin{array}{cc}2&8\\7&4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/u2n9meqn4kjmpoumavo7gjg4xgh0ekbjwu.png)
![-j\left[\begin{array}{cc}0&8\\8&4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/y3epemqtotjdgux1qbc2ezbrvtsu8ef8j0.png)
![+k\left[\begin{array}{cc}0&2\\8&7\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nr785xbpsz533kuadnpyb5g7btrr5ab7vv.png)
Calculate the product
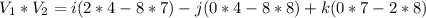
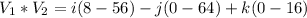
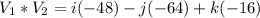
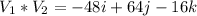
So, the resulting vector, n is:
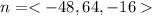
Recall that:
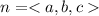
By comparison:
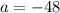
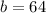
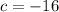
Substitute these values in
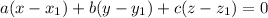
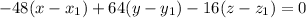
Recall that:
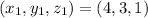
So, we have:

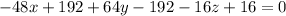
Collect Like Terms
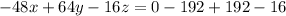
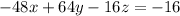
Divide through by -16
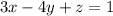
Hence, the equation of the plane is