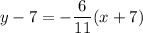Answer:

Explanation:
Step 1: Find the slope
Define the points:
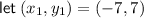
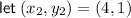
Use the slope formula to find the slope:
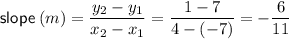
Step 2: Find the equation
Use the found slope from step 1 together with one of the given points in the point-slope form of a linear equation:
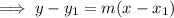
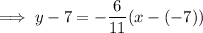
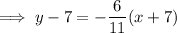
Conclusion
Therefore, the equation of the line that passes through the points (-7, 7) and (4, 1) is: