Question

In ΔABC, m angle CAB = 60°, AD is the angle bisector of angle BAC with D∈BC and AD = 8ft. Find the distances from point D to the sides of the triangle. PLEASE HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

As D lies on BC, the distance from D to BC is 0.

If we let the distance from D to AB be x, then in the right triangle,

`\sin 30^(\circ)=(x)/(8)\\\\(1)/(2)=(x)/(8)\\ \\ x=4`

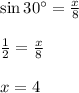
This means the distance from D to side AB is 4.

We can note that
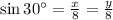`\sin 30^(\circ)=(x)/(8)=(y)/(8)`, meaning y=4 as well, and thus the distance from D to side AC is 4