Question

Write in logarithmic form:
`5^(-1)/(2) = (√(5) )/(5)`

Answer 1

Left-hand side:
`\displaystyle -(1)/(2)\, \ln(5)`.

Right-hand side:
`\displaystyle (1)/(2)\, \ln(5) - \ln(5)`.

Explanation:

Apply the logarithm power rule:
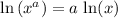`\ln \left(x^(a)\right) = a\, \ln (x)` for all
`x >0`.

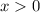This property is not only true for logarithm to the base
`e`, but for other bases, as well.

Take the logarithm (to the base
`e`) of the left-hand side of this equation:

`\displaystyle \ln \left(5^(-1/2)\right) = (-1/2)\, \ln(5)`.

For the right-hand side of this equation, consider the logarithm quotient rule:

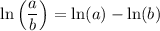`\displaystyle \ln \left((a)/(b)\right) = \ln(a) - \ln (b)` for all
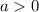`a> 0` and
`b > 0`.

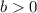Indeed, on the right-hand side of this equation,
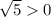`√(5) > 0` and
`5 > 0`. Therefore:

`\displaystyle \ln\left((√(5))/(5)\right) = \ln\left(√(5)\right) - \ln(5)`.

This expression could be further simplified. Notice that
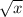`√(x)` is equivalent to
`x^(1/2)` for all
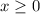`x \ge 0`. (Think about how
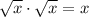`√(x) \cdot √(x) =x` whereas
`x^(1/2) \cdot x^(1/2) = x^((1/2) + (1/2)) = x`.)

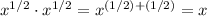Therefore,
`\ln \left(√(5)\right)` would be equivalent to
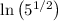`\ln\left(5^(1/2)\right)`. Apply the logarithm power rule to show that
`\displaystyle \ln\left(5^(1/2)\right) = (1)/(2)\, \ln(5)`.

`\begin{aligned} \text{R.H.S.} &= \ln\left((√(5))/(5)\right) \\ &= \ln\left(√(5)\right) - \ln(5) \\ &= (1)/(2)\, \ln(5) - \ln (5) = -(1)/(2)\, \ln(5)\end{aligned}`.

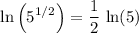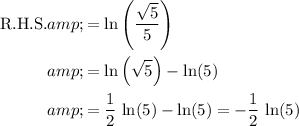Indeed, the left-hand side of this equation matches the right-hand side.