Answer:

Step-by-step explanation:
Hello!
In this case, since the molar mass of a gas mixture can be computed as a weighted average containing mole fractions:
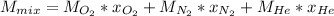
Now, since we are given the by mass percent of each gas, by assuming 1 g of mixture, we therefore have 0.20 g of oxygen, 0.2 g of nitrogen and 0.6 g of helium; next we compute the moles of each gas:
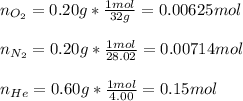
Next, we compute the mole fractions:

Now, we compute the molar mass of the mixture as follows:
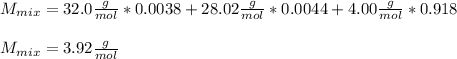
Best regards!