Question

You have 50 ft of fencing and want to fence in a rectangular area of 144 ft^2. What are going to

be the dimensions of the rectangular area?
Quadratic equation

Answer 1

p = 2(l +w)

l= p÷2 -w = l= 25 -w

A= l x w =( 25 -W)W= 144

-w^2 +25w-144 =0

-w^2 +9w+16w- 144=0

(-w^2+9w) +(16w- 144) =0

-w(w - 9) + 16(w - 9) =0

(-w +16) = 0 or w - 9 =0

w = 9 or w = 16

so l = 25 - 9 = 16

or l = 25 - 16 = 9

therefore l = 16ft and w= 9ft

Answer 2

16 by 9 feet.

Explanation:

We have 50 feet of fencing in total.

Therefore, the perimeter of our area is 50. Perimeter is given by:

`P=2(\ell+w)`

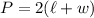
Substituting 50 for P yields:

`50=2(\ell+w)`

And dividing both sides by 2 yields:

`\ell+w=25`

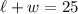
The area of a rectangular is given by:

`A=\ell w`

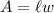
Where
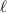`\ell` is the length and
`w` is the width.

We want to enclose 144 feet squared. So, A=144:

`144=\ell w`

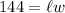
By the perimeter equation, we can subtract a variable, say
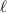`\ell` from both sides. Hence:

`w=25-\ell`

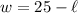
Now, we can substitute this into our area equation. Therefore:

`144=\ell(25-\ell)`

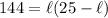
Distribute:

`144=25\ell-\ell^2`

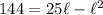
Subtract 144 from both sides:

`-\ell^2+25\ell-144=0`

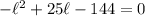
Divide everything by -1:

`\ell^2-25\ell +144=0`

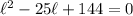
Factor:

`(\ell-9)(\ell-16)=0`

Zero Product Property:

`\ell_1=9\text{ or } \ell_2=16`

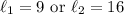
Then it follows that:

`w_1=25-(\ell_1)=25-9=16`

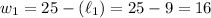
Or:

`w_2=25-(\ell_2)=25-(16)=9`

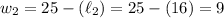
Regardless, the dimensions of the rectangular area will be 16 by 9 feet.