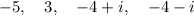Wich of the following is the complete list of roots for the polynomial function f(x) = (x²+2x-15) (x²+8x+17)? -5, 3 -5, 3, -4 + i, -4-i -5, 3, -4+1, 4+i -4+i,-4-i

Question

asked Mar 27, 2023 124k views

1 Answer

Dwalldorf · Answer 1 · 2023-03-31T07:58:58+0000

Answer:

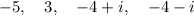
$-5, \quad 3, \quad -4+i,\quad -4-i$

Explanation:

Roots occur when f(x) = 0

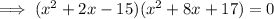
$\implies (x^2+2x-15)(x^2+8x+17)=0$

First trinomial

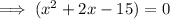
$\implies (x^2+2x-15)=0$

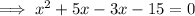
$\implies x^2+5x-3x-15=0$

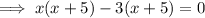
$\implies x(x+5)-3(x+5)=0$

$\implies (x-3)(x+5)=0$

Therefore, roots are 3 and -5

Second trinomial

The second trinomial cannot be factored, so solve using the quadratic formula:

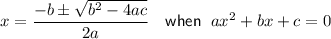
$x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0$

Given:
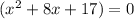
(x^2+8x+17)=0

Therefore: a = 1, b = 8 and c = 17

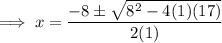
$\implies x=(-8 \pm √(8^2-4(1)(17)))/(2(1))$

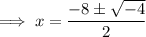
$\implies x=(-8 \pm √(-4))/(2)$

$\implies x=(-8 \pm √(4)√(-1))/(2)$

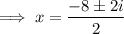
$\implies x=(-8 \pm 2i)/(2)$

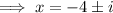
$\implies x=-4 \pm i$

So the roots of the second trinomial are -4 + i and -4 - i

Therefore, the complete list of roots for the given polynomial function are:

$-5, \quad 3, \quad -4+i,\quad -4-i$