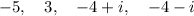Question

Wich of the following is the complete list of roots for the polynomial function f(x) = (x²+2x-15) (x²+8x+17)?

-5, 3
-5, 3, -4 + i, -4-i
-5, 3, -4+1, 4+i
-4+i,-4-i

Answer 1

`-5, \quad 3, \quad -4+i,\quad -4-i`

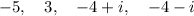
Explanation:

Roots occur when f(x) = 0

`\implies (x^2+2x-15)(x^2+8x+17)=0`

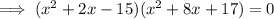
First trinomial

`\implies (x^2+2x-15)=0`

`\implies x^2+5x-3x-15=0`

`\implies x(x+5)-3(x+5)=0`

`\implies (x-3)(x+5)=0`

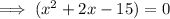
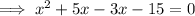
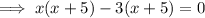
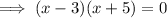
Therefore, roots are 3 and -5

Second trinomial

The second trinomial cannot be factored, so solve using the quadratic formula:

`x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

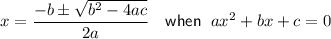
Given:
`(x^2+8x+17)=0`

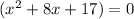
Therefore: a = 1, b = 8 and c = 17

`\implies x=(-8 \pm √(8^2-4(1)(17)))/(2(1))`

`\implies x=(-8 \pm √(-4))/(2)`

`\implies x=(-8 \pm √(4)√(-1))/(2)`

`\implies x=(-8 \pm 2i)/(2)`

`\implies x=-4 \pm i`

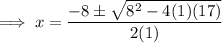
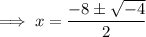
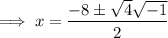
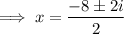
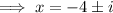
So the roots of the second trinomial are -4 + i and -4 - i

Therefore, the complete list of roots for the given polynomial function are:

`-5, \quad 3, \quad -4+i,\quad -4-i`