Answer:
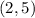
Explanation:
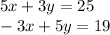
To solve this system of equations, we can first start by solving for one of the two variables in one of the equations. Let's use the first equation to solve for our
 value:
value:
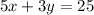
Subtract
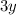 from both sides of the equation:
from both sides of the equation:
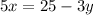
Divide both sides of the equation by the coefficient of
 , which is
, which is
 :
:

Now that we have our
 value, we can substitute it into the second equation to solve for our
value, we can substitute it into the second equation to solve for our
 value:
value:

Substitute:

Distribute the
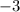 into the parentheses:
into the parentheses:
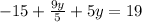
Combine the fractions by achieving a common denominator between
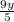 and
and
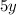 . (Multiply
. (Multiply
 by
by
 ):
):
 ×
×

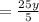
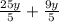
=
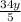
The equation now looks like:
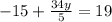
Multiply both sides of the equation by
 to get rid of the fraction:
to get rid of the fraction:
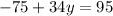
Add
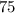 to both sides of the equation:
to both sides of the equation:

Divide both sides of the equation by the coefficient of
 , which is
, which is
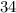 :
:
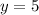
Now with our
 value, we can substitute into the equation representative of the
value, we can substitute into the equation representative of the
 value:
value:

Substitute:
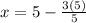
Multiply:

Divide:
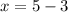
Subtract:

Therefore, the two roads intersect at the position
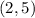 .
.
-
You can check your work by substituting the solved variable values into the initial system of equations:
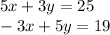
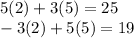
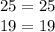
Since the sides of the equations are equal to each other, our solution is correct!