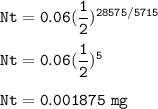Question

Carbon-14 has a half-life of 5715 years. It is used to determine the age of

ancient objects. If a sample today contains 0.060 mg of carbon-14, how much
carbon-14 will be present after 28,575?

Answer 1

The sample of Carbon-14 after 28,575 years=0.001875 mg

Further explanation

General formulas used in decay:

`\large{\boxed{\bold{N_t=N_0((1)/(2))^{T/t(1)/(2) }}}`

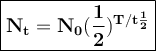
T = duration of decay

t 1/2 = half-life

N₀ = the number of initial radioactive atoms

Nt = the number of radioactive atoms left after decaying during T time

Carbon-14 has a half-life of 5715 years, so t1/2=5715 years

A sample today contains 0.060 mg of carbon-14, so No=0.06 mg, then :

`\tt Nt=0.06((1)/(2))^(28575/5715)\\\\Nt=0.06((1)/(2))^5\\\\Nt=0.001875~mg`