Question

HELP PLS I FORGOT LOL TYSM!

Megan argues that (5m-3)+(2m+4) models the closure property. What reasoning could Megan use to argue that addition of polynomials is closed?


A.) The coefficients of the sum are whole numbers and the

sum is a polynomial.


B.) The coefficients of the product are integers and the product is a polynomial.


C.) The exponents of the sum are whole numbers and the sum is a polynomial.


D.) The exponents of the sum are integers and the sum is a polynomial.


E.) The terms in the expression are rational numbers in the sum is a polynomial.

Answer 1

A. The coefficients of the sum are whole numbers and the sum is a polynomial.

Explanation:

The approach to demonstrate the closure property for the sum consists in defining what a polynomial is and demonstrate that the sum of two polynomials with integer coefficients is equal to a polynomial with integer coefficients. We proceed to show the proof below:

1)
`5\cdot m -3`,
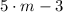`2\cdot m + 4` Given

2)
`(5\cdot m -3)+(2\cdot m +4)` Definition of addition

3)
`(5\cdot m +2\cdot m ) +[(-3)+4]` Definition of substraction/Associative and Commutative properties

4)
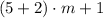`(5+2)\cdot m +1` Distributive property/Definition of substraction

5)
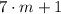`7\cdot m +1` Definition of addition/Result

Hence, the coefficients of the sum are whole numbers and the sum is a polynomial. The correct answer is A.