Answer:
f(x) is positive for all x > 10
Explanation:
Given function:
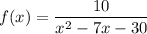
Asymptote
Asymptote: a line which the curve gets infinitely close to, but never touches.
Factor the denominator of the function to find the vertical asymptotes:
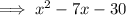
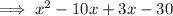
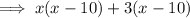
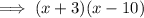
Therefore:
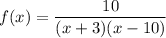
The function is undefined when the denominator is equal to zero.
Therefore, there are vertical asymptotes at x = -3 and x = 10
and a horizontal asymptote at y = 0
f(x) is positive for (10, ∞)
f(x) is negative for (-3, 10)
f(x) is positive for (-∞, -3)