Answer:
The values of a and b are 1 and -8
Explanation:
Let us solve the question by comparing the two sides.
∵ x² + 2x - 7 = (x + a)² + b
→ Let us solve the bracket on the right side
∵ (x + a)² = (x)(x) + 2(x)(a) + (a)(a)
∴ (x + a)² = x² + 2ax + a²
→ Substitute it in the right side above
∴ x² + 2x - 7 = x² + 2ax + a² + b
→ Compare the like terms on both sides (terms of x², terms of x
and numerical terms)
∵ The terms of x are 2x and 2ax
→ Equate them
∵ 2x = 2ax
→ Divide both sides by 2x
∴
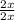 =
=
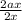
∴ 1 = a
∴ The value of a = 1
∵ The numerical terms are -7 and a² + b
→ Equate them
∵ -7 = a² + b
→ Substitute a by 1
∴ -7 = (1)² + b
∴ -7 = 1 + b
→ Subtract 1 from both sides
∵ -7 - 1 = 1 - 1 + b
∴ -8 = b
∴ The value of b = -8
∴ The values of a and b are 1 and -8