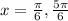Question

Find all solutions of the equation in the interval [0, 2pi).

4cos²x = 5-4 sinx
Write your answer in radians in terms of .
If there is more than one solution, separate them with commas.(PLEASE HURRY)

Answer 1

Explanation:

First, use the Pythagorean identity that says

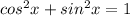`cos^2x+sin^2x=1` and solve it for cos-squared x:

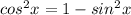`cos^2x=1-sin^2x` so make that replacement into the original equation:

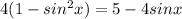`4(1-sin^2x)=5-4sinx` and then distribute to get

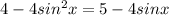`4-4sin^2x=5-4sinx` then get everything on one side so you can factor:

`4sin^2x-4sinx+1=0`

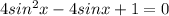
For the sake of ease, let

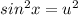`sin^2x=u^2` so sinx = u. Now we are factoring

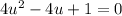`4u^2-4u+1=0` which factors very nicely to

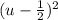`(u-(1)/(2))^2` Now replace the u with sin(x) and solve for where, on the unit circle, the sin of the angle is equal to 1/2:

`sinx=(1)/(2)` when

`x=(\pi )/(6) ,(5\pi)/(6)`