Question

Ernie calculated the slope between two pairs of points. He found that the slope between (-1, 4) and (0, 0) is -4. He also found that the slope between (2, 7) and (3, 3) is -4. Ernie concluded that all of these points are on the same line. Use the drop-down menus to complete the statements about Ernie's conclusion.

Answer 1

Both points do not lie on the same line

Explanation:

There's no drop down to select from. However, I'll answer the question based on whether Ernie's conclusion is correct or not.

Given

Point 1:

(-1,4) and (0,0)

Slope: m = -4

Point 1:

(2,7) and (3,3)

Slope: m = -4

To determine if this conclusion is right or wrong; first, we need to determine the equation of both points using:

`y - y_1 = m(x - x_1)`

For Point 1

`(-1,4)` ---
`(x_1,y_1)`

`(0,0)` ---
`(x_2,y_2)`

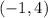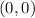Slope:
`m = -4`

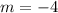
`y - y_1 = m(x - x_1)` becomes

`y - 4 = -4(x - (-1))`

`y - 4 = -4(x +1)`

`y - 4 = -4x -4`

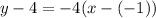
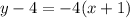
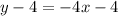
Add 4 to both sides

`y - 4 + 4= -4x -4 + 4`

`y = -4x`

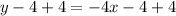
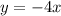
For Point 2:

`(2,7)` ---
`(x_1,y_1)`

`(3,3)` ---
`(x_2,y_2)`

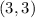Slope:
`m = -4`

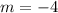
`y - y_1 = m(x - x_1)` becomes

`y -7 = -4(x - 2)`

`y -7 = -4x + 8`

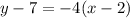
Add 7 to both sides

`y -7 +7= -4x + 8 + 7`

`y = -4x + 15`

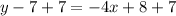
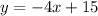
Comparing both equations:

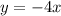`y = -4x` and
`y = -4x + 15`

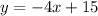
Both expressions are not equal.

Hence, both points do not lie on the same line