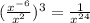Answer:
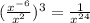
Explanation:
Given
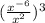
Required
Determine the equivalent expression
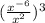
First, we need to evaluate the expression in the bracket:
Apply the following law of indices:
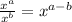
So:
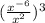 becomes
becomes
=
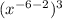
=
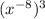
Open the bracket
=
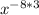
=
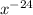
Convert the above expression to fraction
=
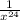
Hence: