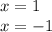Question

Help !



`\quad \sf \: {x}^(2) = 1`

find the value of x ​

Answer 1

`x=1`

`x=-1`

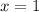
Explanation:

Let's use the quadratic formula to solve this.

Quadratic formula is usually defined as the formula for determining the roots of a quadratic equation from its coefficient. Quadratic equations are equations containing a single variable of degree 2. Its general form is ax^2 + bx + c = 0, where x is the variable, and a,b, and c are constants (a ≠ 0).

_______

steps

1 ) move terms to the left side

`x^2=1`

`x^2-1=0`

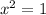
2) Use the quadratic formula

`x=(-b\pm√(b^2-4ac) )/(2a)`

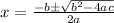
Once in standard form, identify a, b, and c from the original equation and plug them into the quadratic formula.

`x^2-1=0`

`a =1 \\b = 0\\c=-1`

`x=(-0\pm√(0^2-4*1(-1)) )/(2*1)`

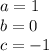
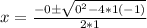
3) Simplify

- evaluate the exponent

`x=(0\pm√(0^2-4*1(-1)) )/(2*1)`

`x=(0\pm√(0-4*1(-1)) )/(2*1)`

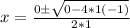
- Multiply the numbers

`x=(0\pm√(0-4*1(-1)) )/(2*1)\\`

`x=(0\pm√(0+4) )/(2*1)`

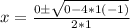
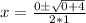
- add the numbers

`x=(0\pm√(0+4) )/(2*1)`

`x=(0\pm√(4) )/(2*1)`

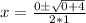
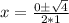
- Evaluate the square root

`x=(0\pm√(4) )/(2*1)`

`x=(0\pm2)/(2*1)`

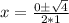
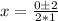
- add zero

`x=(0\pm2)/(2*1)`

`x=(\pm2)/(2*1)`

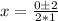
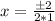
- Multiply the numbers

`x=(\pm2)/(2*1)`

`x=(\pm2)/(2)`

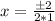
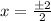
4) separate the equations

- To solve for the unknown variable, separate into two equations: one with a plus and the other with a minus.

`x=(2)/(2)\\x=(-2)/(2)`

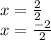
5) solve

- Rearrange and isolate the variable to find each solution

`x=1\\x=-1`

___________

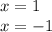
solution

`x=1\\x=-1`