Question

asked Mar 3, 2023 139k views

2 Answers

Wibbly · Answer 1 · 2023-03-04T17:42:14+0000

Solution :

put x = 1,

it's value is 0.

hence, it's a solution

divide 2x³ - x² + x - 2 by (x - 1)

it can be written as :

Vegar Westerlund · Answer 2 · 2023-03-08T02:42:44+0000

Answer:

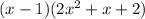
(x-1)(2x^2+x+2)

Explanation:

Factorize:

f(x)=2x^3-x^2+x-2

Factor Theorem

If f(a) = 0 for a polynomial then (x - a) is a factor of the polynomial f(x).

Substitute x = 1 into the function:

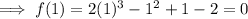
$\implies f(1)=2(1)^3-1^2+1-2=0$

Therefore, (x - 1) is a factor.

As the polynomial is cubic:

$\implies f(x)=(x-1)(ax^2+bx+c)$

Expanding the brackets:

$\implies f(x)=ax^3+bx^2+cx-ax^2-bx-c$

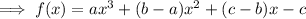
$\implies f(x)=ax^3+(b-a)x^2+(c-b)x-c$

Comparing coefficients with the original polynomial:

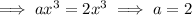
$\implies ax^3=2x^3 \implies a=2$

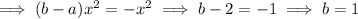
$\implies (b-a)x^2=-x^2 \implies b-2=-1 \implies b=1$

$\implies -c=-2 \implies c=2$

Therefore:

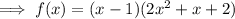
$\implies f(x)=(x-1)(2x^2+x+2)$

Cannot be factored any further.