Question

Sushil, Alex and Peter share some sweets in the ratio 6:5:1. Sushil gets 60 more sweets than Peter. How many sweets are there altogether?

Answer 1

There are 144 sweets altogether.

Explanation:

Let us call:

S = Number of sweets Sushil's sweets

A = Number of sweets Alex' sweets

P = Number of sweets Peter's sweets

The ratio between them is S:A:P = 6:5:1. It must be separated as:

`\displaystyle (S)/(A)=(6)/(5)`

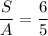
Or, equivalently:

5S = 6A [1]

Also:

`\displaystyle (A)/(P)=(5)/(1)`

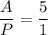
Or, equivalently:

A = 5P [2]

We also know Sushil gets 60 more sweets than Peter:

S = P + 60 [3]

Solving for P:

P = S - 60 [4]

Substituting in [2]:

A = 5(S - 60) = 5S - 300 [5]

Substituting in [1]

5S = 6(5S - 300)

Operating:

5S = 30S - 1800

Rearranging:

25S = 1800

Dividing by 25:

S = 1800/25=72

S = 72

Substituting in [5]:

A = 5(72) - 300

A = 60

Substituting in [4]:

P = 72 - 60

P = 12

In total there are 72 + 60 + 12 = 144.

There are 144 sweets altogether.