Question

Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 4x and y = 2x−2 intersect are the solutions of the equation 4x = 2x−2. (4 points)

Part B: Make tables to find the solution to 4x = 2x−2. Take the integer values of x between −3 and 3. (4 points)

Part C: How can you solve the equation 4x = 2x−2 graphically? (2 points)

Answer 1

This is why because

• y=4x
• y=2x-2

So y is equal hence both sides are equal

so x values are equal

Tables

#4x=2x-2

`\boxed{\begin{array}c\bf x&\bf 4x &\sf 2x-2\\ \sf -3 &\sf -12&\sf 4 \\ \sf -2&\sf -8&\sf 6\\ \sf -1&\sf -4&\sf -4\\ \sf 0&\sf 0&\sf -2\\ \sf 1&\sf 4&\sf 0 \\ \sf 2&\sf 8&\sf 2\\ \sf 3&\sf 12&\sf 4 \end{array}}`

Let's solve

Graph both

The solution is (-1,-4)

The reason is -1 has same y values for both functions

Answer 2

Part A

One method for solving a system of equations is solving by substitution.

Substitute the variable in one equation with the expression of the variable in the other equation.

Replace the y of "y = 2x - 2" with "y = 4x" to make "4x = 2x - 2".

Part B

`\large\begin{array} c \cline{1-3} x & 4x & 2x-2 \\\cline{1-3} 3 & 12 & 4\\\cline{1-3} 2 & 8 & 2\\\cline{1-3} 1 & 4 & 0\\\cline{1-3} 0 & 0 & -2\\\cline{1-3} -1 & -4 & -4\\\cline{1-3} -2 & -8 & -6\\\cline{1-3} -3 & -12 & -8\\\cline{1-3} \end{array}`

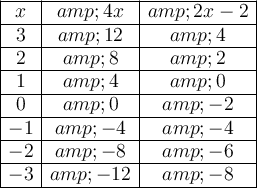
The only integer for which both equations give the same result is x = -1.

Therefore, the solution is x = -1

Part C

To solve the equation graphically, graph the lines y = 4x and y = 2x - 2.

The x-coordinate of the point of intersection is the solution to the equation 4x = 2x - 2

(see attached)