Question

.Given logb^3 = 1/4 what is logb^9

Answer 1

1/2

Explanation:

Find the domain of the inequality:
`\left \{ {{b > 0} \atop {b\\eq 1}} \right.`

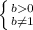
Solve the inequality: b > 0

Convert inequality to equation: b = 1

Solve the equation: b = 1

Convert equation to inequality: b ≠ 1

Find the intersection: 0 < b < 1 or b > 1

The domain of the inequality is:
`\text{log}_b3=(1)/(4) ,0 < b, < b < 1` or
`b > 1`

Convert logarithm to exponential form:
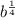`b^{(1)/(4) }` = 3, 0 <b<b1 or b > 1

Power on both sides: (b^1/4)^4=3^4, 0<b<1 or b > 1

Simplify using exponent rule (a^n)^m = a^nm:

b = 3^4, 0<b<1 or b > 1

Calculate the power:

b = 81 , 0<b<1 or b > 1

Find the intersection: b = 81

Substitute:
`\text{log}_(81)9`

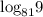
Factorize the argument:
`\text{log}_(81) 3^2`

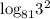
Express the logarithm of a power of an expression as the power times the logarithm of the expression:
`2*\text{log}_(81) 3`

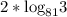
Factorize the base:
`2*\text{log}x_(3^4) 3`

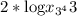
Rewrite the expression using the formula:
`\text{log}_(a^n) b`

to
`((1)/(n) ) \text{log}_ab:`
`2*(1)/(4) *\text{log}_33`

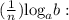
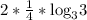
Apply the power law of logarithm to simplify the expression:

`2*(1)/(4)`

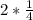
Reduce the expression to the lowest form:

`(1)/(2)`

Answer: 1/2

Answer 2

`\log_b9=(1)/(2)`

Explanation:

`\textsf{Given}: \quad\log_b3=(1)/(4)`

`\textsf{To find }\log_b9, \textsf{ rewrite 9 as 3}^2:`

`\implies \log_b9=\log_b3^2`

`\textsf{Apply the Power log law}: \quad \log_ax^n=n\log_ax`

`\implies \log_b3^2= 2\log_b3`

`\begin{aligned}\textsf{If }\log_b3& =(1)/(4)\\\\ \implies 2 \log_b3 & =2 * (1)/(4)\\\\ & = (2)/(4)\\\\ & = (1)/(2)\end{aligned}`

`\textsf{Therefore}: \quad\log_b9=(1)/(2)`