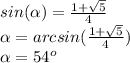Question

Find the acute triangle Alpha
when cos 3 Alpha=- Sin 2 Aplha ​

Answer 1

Alpha is 54 degrees

Explanation:

We can use the addition identities for cosine and for sine to express the given equation in terms of sine and cosine of alpha:

`cos(3\alpha)= - sin(2\alpha)\\cos(2\alpha)*cos(\alpha)-sin(2\alpha)*sin(\alpha) = - 2*sin(\alpha)*cos(\alpha)\\(cos^2(\alpha)-sin^2(\alpha))*cos(\alpha)-2*sin^2(\alpha)*cos(\alpha)+ 2*sin(\alpha)*cos(\alpha)=0\\cos^2(\alpha)-sin^2(\alpha)-2*sin^2(\alpha)+ 2*sin(\alpha)=0\\1-sin^2(\alpha)-sin^2(\alpha)-2*sin^2(\alpha)+2*sin(\alpha)=0\\-4*sin^2(\alpha)+2*sin(\alpha)+1=0`

we can use the quadratic formula to find what sine of alpha is:

`sin(\alpha)=(-2+/-√(4-4(-4)(1)) )/(2(-4)) =(-1+/-√(5) )/(-4)`

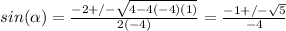
and for
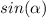`sin(\alpha)` to be positive (acute angle in the first quadrant) the answer is:

`sin(\alpha)=(1+√(5) )/(4) \\\alpha= arcsin((1+√(5) )/(4))\\\alpha= 54^o`